掌握12x13的竖式计算技巧,轻松解题!
在进行数学运算时,竖式计算是一种直观且有效的方法,尤其适用于乘法运算。今天,我们将详细解析12乘以13的竖式计算方法,通过这一具体例子,帮助大家更好地理解和掌握这一技能。

首先,我们需要准备两个乘数:12和13。在竖式计算中,我们通常将较小的数放在上方作为被乘数,较大的数放在下方作为乘数,但这不是硬性规定,关键在于个人习惯和清晰表达。这里,我们按照12在上、13在下的方式排列。

步骤一:个位相乘
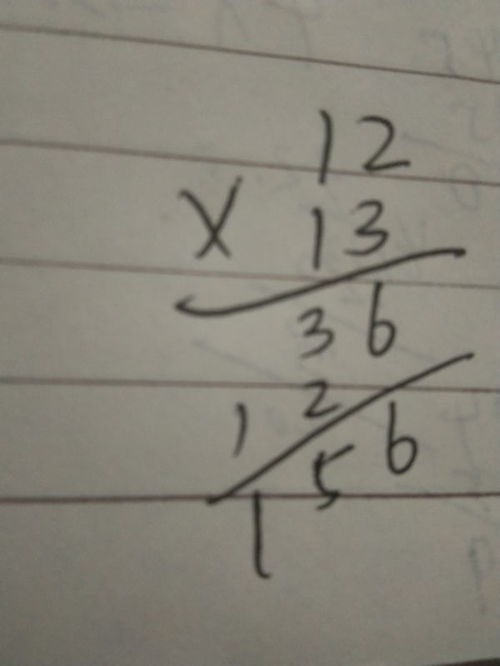
从个位开始,我们将12的个位数字2与13的个位数字3相乘。2乘以3等于6,这个结果直接写在竖式计算的最右侧,代表乘积的个位数字。
步骤二:十位相乘(不进位)
接下来,我们将12的十位数字1(实际上代表10)与13的个位数字3相乘。10乘以3等于30。由于我们还没有处理进位,所以暂时将30写在6的左侧,但注意,这里的3实际上代表30的十位数字,而0则暂不写入,因为我们需要考虑下一步的进位情况。
步骤三:处理进位
在步骤二中,我们得到的30实际上需要与步骤一中得到的6相加,以得到完整的乘积的一部分。但在这里,我们采用竖式计算的“分步处理”策略,先记录3(十位数字),然后处理进位。6加上30的个位0等于6,但这个6实际上需要与下一步的结果相加,因为我们还没有完成整个乘法过程。然而,在这一步,我们主要关注进位到更高位的数字。由于30的十位是3,没有进位到更高位,所以我们暂时不需要在更高位上添加任何数字。
但值得注意的是,这里的“不进位”是相对于更高位而言的。对于当前位(十位),我们确实有一个进位(从个位6到十位,但实际上这个进位是在下一步与更高位相乘时一并考虑的),但在竖式计算中,我们通常将这种进位视为下一步计算的一部分,而不是立即写入结果中。
步骤四:十位相乘(考虑进位)
现在,我们将12的十位数字1(代表10)与13的十位数字1相乘。10乘以10等于100,但由于我们在步骤三中知道有个位进位的6(实际上是从个位2乘以3得到的6,再加上30的个位0,但这里的进位是在与更高位相乘时一并考虑的),我们需要将这个进位加到100上。然而,在竖式计算中,我们通常不会立即进行这个加法,而是先记录100的百位和十位(这里是0和1,因为100的个位0在与更低位的进位相加时会被考虑),然后在下一步处理进位。
但在这个特定例子中,由于我们只有一个进位6(远小于100),所以我们实际上不需要在百位上添加任何数字(因为6不足以让100的百位数字增加)。然而,我们需要将这个进位6加到100的十位上(如果有的话),但在这里,100的十位本身就是0(因为100没有十位数字,除了0以外),所以我们实际上是将6加到下一个更低位的计算中(如果有的话)。但在这个例子中,下一个更低位就是我们已经计算过的个位和十位(6和30/3),而进位6已经在这个过程中被考虑过了(通过步骤三的“不进位”说明和这里的“考虑进位”说明相结合来理解)。
为了避免混淆,我们可以这样理解:在竖式计算中,我们通常不会立即处理所有进位,而是将它们视为下一步计算的一部分。在这个例子中,步骤三中的进位6实际上是在与13的十位相乘时(即步骤四)被一并考虑的,但由于6远小于100(10乘以10的结果),所以我们不需要在百位上添加任何数字。而十位上的进位(如果有的话)实际上是在与更低位的计算中(如果有的话)被处理的,但在这个例子中,我们已经完成了所有必要的计算。
步骤五:整理结果
现在,我们可以将之前计算得到的各个部分组合起来,得到最终的结果。从右往左,我们依次有:个位6(来自2乘以3)、十位3(来自10乘以3的十位部分,加上之前步骤的进位后没有变化)、百位和千位(实际上在这个例子中只有百位是有效的,来自10乘以10的1加上之前步骤的进位6后的结果,但6不足以让百位数字增加,所以百位仍然是1,而千位是0,因为12乘以13的结果小于1000)。因此,最终结果是156。
通过上面的详细步骤,我们可以看到竖式计算虽然看似复杂,但实际上每一步都有明确的逻辑和规则可循。只要掌握了这些规则,就可以轻松地进行任何两位数的乘法运算。希望这篇文章能够帮助大家更好地理解和掌握竖式计算方法,提高数学运算能力。
- 上一篇: 《战舰少女R》无畏之海决战全攻略,助你征服波涛!
- 下一篇: 龙之谷90版本黑暗复仇者如何加点刷图?
-
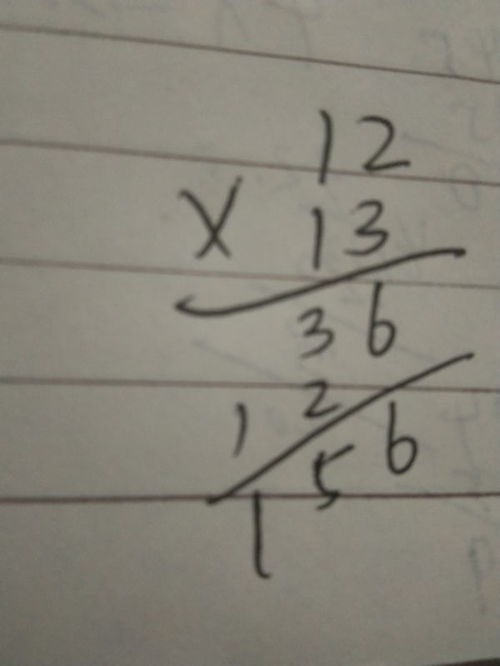 掌握12x13的竖式计算技巧,轻松解题资讯攻略11-10
掌握12x13的竖式计算技巧,轻松解题资讯攻略11-10 -
 掌握英语四级高效答题顺序,解题技巧助你一次过关!资讯攻略11-07
掌握英语四级高效答题顺序,解题技巧助你一次过关!资讯攻略11-07 -
 CAD技巧:轻松掌握面积计算方法!资讯攻略11-07
CAD技巧:轻松掌握面积计算方法!资讯攻略11-07 -
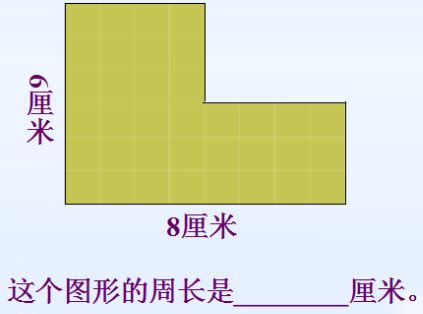 右边图形周长的计算过程是多少厘米?资讯攻略12-02
右边图形周长的计算过程是多少厘米?资讯攻略12-02 -
 掌握PcAnywhere的实用技巧:轻松远程操控资讯攻略11-15
掌握PcAnywhere的实用技巧:轻松远程操控资讯攻略11-15 -
 Excel高手必学:轻松掌握表格中乘积的计算方法!资讯攻略11-16
Excel高手必学:轻松掌握表格中乘积的计算方法!资讯攻略11-16











