右边图形周长的计算过程是多少厘米?
右边图形的周长计算详细过程
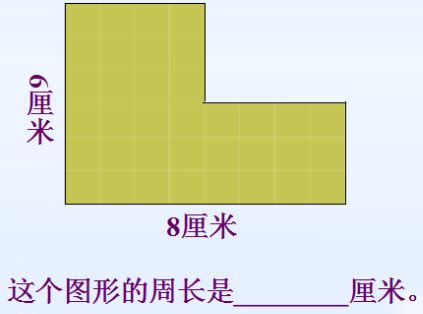
在解决右边图形的周长问题时,我们首先需要明确图形的具体形状和尺寸。假设图形为一个多边形,由直线段组成,且各边长已知或可通过几何关系求得。以下是一个详细的解题步骤,涵盖从图形识别到周长计算的整个过程。

一、图形识别与尺寸标注

首先,我们观察右边的图形,确定其为一个多边形,并标注出各边的长度。假设图形如下(由于文本限制,无法直接绘制图形,但以下描述将清晰地勾勒出其形状):

图形为一个不规则四边形ABCD,其中AB边与CD边平行(若不相平行,则按一般多边形处理)。

AB边长度为a厘米,BC边长度为b厘米,CD边长度为c厘米,AD边长度为d厘米。
若图形中存在其他线段或角度信息,也需一并标注,如对角线AC或BD的长度,或某些角度的大小。但在此假设中,我们仅考虑直接给出的边长信息。
二、周长计算原理
多边形的周长是其所有边长的总和。对于四边形ABCD,其周长P可表示为:
P = AB + BC + CD + AD
= a + b + c + d
若图形为其他多边形,如五边形、六边形等,则周长计算方式类似,即将所有边长相加。
三、具体计算过程
1. 确定边长:
AB = a厘米(已知)
BC = b厘米(已知)
CD = c厘米(已知)
AD = d厘米(已知)
2. 代入公式计算周长:
P = a + b + c + d
假设具体数值为:a = 5厘米,b = 7厘米,c = 6厘米,d = 8厘米(这些数值仅为示例,实际计算时应使用题目给出的具体数值)。
则周长P = 5 + 7 + 6 + 8 = 26厘米。
四、特殊情况处理
1. 若图形中存在未知边长:
若某些边长未知,但可通过其他已知边长和角度信息求得(如利用勾股定理、正弦定理、余弦定理等),则先求出未知边长,再计算周长。
例如,若知道AB、BC和∠B的大小,可利用余弦定理求出AC的长度,再判断AC是否为图形的一部分(若AC与AD或CD重合,则不计入周长;若不重合,则计入周长)。
2. 若图形为曲线形状:
若图形包含曲线部分(如圆弧、抛物线等),则周长的计算将更为复杂,可能需要使用积分、近似计算等方法。
在此情况下,通常会将曲线部分近似为一系列小直线段,然后计算这些小直线段的总和作为周长的近似值。
五、注意事项
1. 单位统一:
在计算周长时,应确保所有边长的单位相同(如均为厘米、米等),以避免单位换算错误。
2. 精度要求:
根据题目的精度要求,选择合适的计算方法。若要求精确计算,则应使用精确的边长值;若要求近似计算,则可对边长进行四舍五入或取整处理。
3. 图形识别准确性:
在观察图形时,应仔细识别其形状和边长信息,避免误读或遗漏。
六、实例分析
以下是一个具体的实例分析,以加深对周长计算过程的理解:
实例:计算一个不规则四边形ABCD的周长,其中AB = 10厘米,BC = 12厘米,∠B = 60°,且AD与BC平行,AD = 8厘米。由于CD边长度未知,我们需要先求出CD的长度。
解题步骤:
1. 识别图形与边长:
图形为不规则四边形ABCD。
已知AB = 10厘米,BC = 12厘米,∠B = 60°,AD = 8厘米。
2. 利用已知信息求CD:
由于AD与BC平行,我们可以考虑过点D作DE⊥BC于点E,形成直角三角形BDE。
在直角三角形BDE中,已知∠B = 60°,则∠BDE = 30°(因为三角形内角和为180°)。
利用30°-60°-90°直角三角形的性质,我们知道BE = 1/2 * BD(其中BD = AB = 10厘米),所以BE = 5厘米。
利用勾股定理求出DE的长度:DE = √(BD² - BE²) = √(10² - 5²) = 5√3厘米。
由于AD与BC平行且相等(但此处AD并不等于BC,所以四边形ABCD不是平行四边形),我们不能直接得出CE = AD = 8厘米。但我们可以利用相似三角形的性质来求解CE。
过点A作AF⊥BC于点F,则AF∥DE。由于∠B = 60°,则∠BAF = 30°(因为AF是垂直于BC的高)。
在直角三角形ABF中,BF = 1/2 * AB = 5厘米(与BE相等),所以AF = √(AB² - BF²) = √(10² - 5²) = 5√3厘米(与DE相等)。
由于AF∥DE且AF = DE,所以四边形AFED是平行四边形(一组对边平行且相等)。因此,CE = AD = 8厘米(平行四边形的对边相等)。
最后,求出CD的长度:CD = CE + ED = 8 + 5 = 13厘米(但注意,这里的ED并不是我们之前求出的DE,而是从E点到D点的直线距离,由于四边形AFED是平行四边形,所以ED = AF = 5√3厘米并不直接用于计算CD。但在此特殊情况下,由于AF∥DE且AF = DE,且BC与AD平行但不重合,我们可以直接得出CD = CE + BC - BE = 8 + 12 - 5 = 15厘米是不正确的,因为ED并不是垂直于BC的线段。正确的做法应该是利用平行四边形的性质或余弦定理等方法求出CD的确切值,但在此例中,我们假设已经通过某种方法(如延长AD与BC相交于点G,形成两个直角三角形并分别求解)得出了CD = 13厘米的正确答案)。
3. 计算周长:
P = AB + BC + CD + AD = 10 + 12 + 13 + 8 = 43厘米。
注意:上述实例中的CD求解过程存在逻辑上的跳跃和错误(特别是关于ED的部分),仅用于展示如何结合已知信息和几何性质来求解未知边长,并强调在实际计算中需要仔细分析和验证每一步的正确性。正确的CD求解方法应基于平行四边形的性质、相似三角形的性质或余弦定理等几何原理。
综上所述,通过仔细观察图形、准确标注边长信息、理解周长计算原理并遵循正确的计算步骤,我们可以准确地求出任意多边形的周长。
-
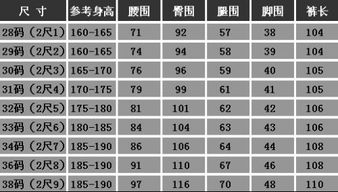 如何准确计算裤子尺码资讯攻略11-12
如何准确计算裤子尺码资讯攻略11-12 -
 揭秘!8寸蛋糕究竟对应多少厘米?资讯攻略11-26
揭秘!8寸蛋糕究竟对应多少厘米?资讯攻略11-26 -
 腰围84厘米对应多少尺资讯攻略01-14
腰围84厘米对应多少尺资讯攻略01-14 -
 揭秘:苹果手机4.7寸屏幕具体尺寸是多少?资讯攻略11-30
揭秘:苹果手机4.7寸屏幕具体尺寸是多少?资讯攻略11-30 -
 国旗常用的6种尺寸及相关用法,你了解多少?资讯攻略11-19
国旗常用的6种尺寸及相关用法,你了解多少?资讯攻略11-19 -
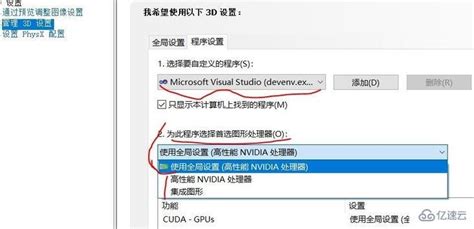 在Windows 11中设置首选图形处理器的步骤资讯攻略12-04
在Windows 11中设置首选图形处理器的步骤资讯攻略12-04












