线性代数:证明若向量α非零则α线性相关
在线性代数的广袤领域中,证明题如同一座座思维的灯塔,引领我们探索向量与矩阵的奥秘。今天,我们聚焦于一个基础而深刻的主题:向量的线性相关性。具体而言,若向量α非零(记为α≠0),则向量α本身线性相关;进一步地,若向量组a1, a2, ..., an中包含零向量或者任意两个向量线性相关,则整个向量组线性相关。这一结论看似简单,实则蕴含着线性代数的基本逻辑与深刻洞见。让我们从多个维度出发,深入剖析这一命题。

一、向量线性相关性的基本概念
首先,明确向量线性相关性的定义是解题的前提。在n维向量空间中,如果存在不全为零的标量k1, k2, ..., kn,使得k1a1 + k2a2 + ... + knan = 0,则称向量组a1, a2, ..., an线性相关。反之,如果只有当k1 = k2 = ... = kn = 0时,上述等式才成立,则称向量组线性无关。
二、单一非零向量的线性相关性
对于单一非零向量α,我们可以直接应用线性相关性的定义进行证明。设α为n维非零向量,即α≠0。显然,存在一个非零标量k(例如k=1),使得kα = α,同时-kα = -α。注意到k和-k不全为零(因为k非零),且kα + (-k)α = 0。这正好符合线性相关的定义,即存在不全为零的标量使得这些标量与向量的线性组合为零向量。因此,单一非零向量α本身是线性相关的。这一结论虽然简单,却揭示了线性相关性概念的宽泛性:即使只有一个向量,也可能因为非零而表现出线性相关性。
三、包含零向量的向量组
接下来,考虑向量组中包含零向量的情况。设向量组为a1, a2, ..., an,其中至少有一个向量(不妨设为ai,i∈{1,2,...,n})为零向量0。此时,我们可以选择一组不全为零的标量k1, k2, ..., kn,其中ki=1(对应ai为零向量的情况),而其余kj(j≠i)均为零。于是,有k1a1 + k2a2 + ... + knan = ki * 0 + k1a1 + ... + k(i-1)a(i-1) + k(i+1)a(i+1) + ... + knan = 0。由于ki=1且ai=0,上述等式显然成立,且标量k1, k2, ..., kn不全为零。因此,包含零向量的向量组线性相关。
四、任意两个向量线性相关的情况
进一步地,若向量组a1, a2, ..., an中存在任意两个向量(不妨设为ai和aj,i≠j)线性相关,我们同样可以证明整个向量组线性相关。设ai和aj线性相关,则存在不全为零的标量m和n,使得mai + nj = 0。此时,我们可以构造一组不全为零的标量k1, k2, ..., kn,其中ki=m(对应ai),kj=n(对应aj),而其余kl(l≠i且l≠j)均为零。于是,k1a1 + k2a2 + ... + knan = mai + nj + k1a1 + ... + k(i-1)a(i-1) + k(i+1)a(i+1) + ... + k(j-1)a(j-1) + k(j+1)a(j+1) + ... + knan = 0。由于mai + nj = 0且ki和kj不全为零,上述等式成立,且标量k1, k2, ..., kn不全为零。因此,整个向量组线性相关。
五、线性相关性的几何意义
从几何角度来看,向量的线性相关性可以理解为向量在向量空间中的位置关系。以二维向量空间为例,如果两个向量共线(即一个向量是另一个向量的倍数),则它们线性相关。这是因为共线的两个向量不能构成一个独立的基,无法张成整个二维空间。类似地,在三维或更高维的向量空间中,如果一组向量中有向量可以由其他向量线性表示,则这组向量线性相关。这种几何直观帮助我们理解为什么包含零向量或任意两个线性相关的向量会导致整个向量组线性相关。
六、线性相关性的代数应用
线性相关性不仅是一个理论概念,还在许多代数应用中发挥着重要作用。例如,在求解线性方程组时,如果系数矩阵的列向量线性相关,则方程组可能有无穷多解或无解。这是因为线性相关的列向量意味着方程组中存在冗余信息,导致解的不唯一性或无解性。此外,在矩阵的秩、特征值、逆矩阵等概念中,线性相关性也扮演着重要角色。
七、结论
综上所述,若向量α非零,则向量α本身线性相关;若向量组a1, a2, ..., an中包含零向量或任意两个向量线性相关,则整个向量组线性相关。这一结论不仅基于线性相关性的定义,还通过几何意义和代数应用得到了进一步阐释。在线性代数的广阔天地里,这一基础命题如同一块基石,支撑起更高深的数学理论与实际应用。通过深入理解和灵活应用这一概念,我们能够更好地把握向量与矩阵的奥秘,探索数学世界的无限可能。
- 上一篇: 如何轻松点亮QQ安全达人图标?
- 下一篇: 如何在最新版QQ中设置九张图的个性名片
-
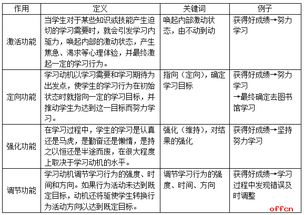 动机强度如何影响工作效率?资讯攻略11-13
动机强度如何影响工作效率?资讯攻略11-13 -
 揭秘:导致《忍者之刃》卡顿的幕后真相!资讯攻略12-05
揭秘:导致《忍者之刃》卡顿的幕后真相!资讯攻略12-05 -
 专业人气非编论坛:聚焦SONY Vegas与EDIUS讨论资讯攻略12-05
专业人气非编论坛:聚焦SONY Vegas与EDIUS讨论资讯攻略12-05 -
 轻松指南:如何在线申请工商营业执照资讯攻略11-28
轻松指南:如何在线申请工商营业执照资讯攻略11-28 -
 DNF押运证明使用全攻略资讯攻略02-03
DNF押运证明使用全攻略资讯攻略02-03 -
 轻松辨别:你的iPad到底是哪一代?资讯攻略11-08
轻松辨别:你的iPad到底是哪一代?资讯攻略11-08












